Quantum Noise: Noise Simulation and Quantum Error Correction using Amazon Braket

Quantum computers rely on the principles of quantum mechanics, which can be difficult to understand and predict due to the inherent uncertainty and noise in quantum systems. In a quantum computer, noise can refer to any unwanted disturbance that can affect the state of the system and the accuracy of its calculations. This noise can come from a variety of sources, including external factors such as temperature and electromagnetic radiation, as well as from within the system itself, such as indefinite control of the quantum bits (qubits) or imperfections in the hardware.

To reduce the effects of noise, quantum computers use error-correcting codes and other techniques to protect the delicate quantum states of the qubits. However, noise is still a major challenge in the development of quantum computers and a key area of research in the field.

There are several steps that researchers and engineers are taking to overcome the challenges of noise in quantum computing. Some of these include:

1. Developing more advanced error-correcting codes: One of the main ways to protect against noise in a quantum computer is to use error-correcting codes, which can detect and correct errors in the quantum states of the qubits. Researchers are working on developing more advanced codes that can better detect and correct errors, even in the presence of significant noise.
2. Improving hardware: Another key approach is to improve the hardware of quantum computers, such as the qubits and other components, to make them more stable and less open to noise. This can involve using different materials or designs that are less affected by external factors.
3. Reducing external sources of noise: Another important step is to reduce the external sources of noise that can affect quantum computers. This can involve using specialized shielding or cooling mechanisms to protect the quantum system from external factors such as temperature and electromagnetic radiation.
4. Developing better simulation and testing tools: To develop and optimize quantum algorithms, researchers need accurate simulation and testing tools that can help them understand how a quantum system will behave in the presence of noise. By developing better simulation and testing tools, researchers can better understand the effects of noise and develop algorithms that are more robust to it.
5. Developing new programming languages and frameworks: Finally, researchers are also working on developing new programming languages and frameworks that make it easier to write and run quantum algorithms. These tools can provide a higher-level interface for working with quantum systems, abstracting away some of the complexity and making it easier to develop algorithms that can cope with noise.

Overall, these advancements are helping to make quantum computing more practical and useful, by enabling researchers to overcome the challenges of noise and other errors in quantum systems.

What is noise simulation?

It is the process of using computer modeling and simulation techniques to study the effects of noise on a quantum system. This can involve using specialized algorithms and software tools to simulate the behavior of a quantum computer in the presence of noise, allowing researchers to study how noise affects the accuracy and performance of quantum algorithms.

Overall, noise simulation is an important tool for advancing the field of quantum computing, and helps researchers to better understand and overcome the challenges of noise in quantum systems.

Error correcting codes

Some common types of error-correcting codes used in quantum computing include:

1. Repetition codes: Repetition codes are the simplest type of error-correcting code, and involve encoding each bit of data multiple times.

For example, a repetition code might encode a single bit of data as three qubits, with each qubit representing the same value. If one of the qubits is flipped by noise, the other two qubits can be used to correct the error.

2.  Parity codes: Parity codes are similar to repetition codes, but instead of encoding each bit multiple times, they use an additional qubit to encode the parity (odd or even) of the data bits.

For example, if the data bits are encoded as qubits 0 and 1, the parity qubit would be encoded as the XOR of qubits 0 and 1. If an error occurs in one of the data qubits, it can be detected and corrected by comparing the value of the parity qubit to the expected value.

3.  Quantum error-correcting codes: Quantum error-correcting codes are more advanced codes that are specifically designed for use in quantum computing. These codes use complex encoding and decoding schemes to protect against errors in the quantum states of the qubits, using techniques such as entanglement and superposition.

Overall, error-correcting codes are an essential tool for protecting against noise and other errors in quantum computing. By using these codes, researchers can improve the accuracy and reliability of quantum algorithms, making them more practical and useful.

Kraus representation

In the Kraus representation, a quantum operation is represented as a set of matrices, known as Kraus operators, that act on the quantum state of the system. These operators represent the different ways that the operation can change the state of the system, and can be used to calculate the final state of the system after the operation has been applied.

It also allows for the easy calculation of the effects of different quantum operations, which is useful for tasks such as error correction and noise simulation in quantum computing. Overall, the Kraus representation is an important tool for understanding and manipulating quantum systems.

Let's deep dive to see how the above represetation is useful in quantum computing noise simulation-

The Kraus representation is useful for quantum computing noise simulation because it provides a detailed and flexible way of representing the effects of quantum operations on a quantum system. By using the Kraus representation, we can simulate the effects of different noise sources on a quantum system, and can study how these effects can be reduced using error-correcting codes and other techniques.

For example-Suppose that a quantum operation is represented by a set of Kraus operators, and that one of these operators is affected by noise. In the Kraus representation, this noise can be modeled as a small disturbance to the operator, which changes its effect on the quantum state. By simulating the operation with and without the disturbance, we can study how the noise affects the final state of the system, and can develop strategies for reducing its impact.

So basically this representation is a powerful tool for studying the effects of noise in quantum computing, and can help to better understand and overcome the challenges of noise in quantum systems.

Suppose that a quantum operation is represented by the Kraus operators A and B, which act on a quantum state |ψ⟩ as follows:

|ψ'⟩ = A|ψ⟩ + B|ψ⟩

Now, suppose that the operator A is affected by noise, which can be modeled as a small disturbance to the operator A:

A' = A + δA

where δA is the noise disturbance.

Kraus representation- |ψ''⟩ = (A + δA)|ψ⟩ + B|ψ⟩

By comparing |ψ'⟩ and |ψ''⟩,  the noise affects the final state of the system can be studied.

That's how the Kraus representation can be used to study the effects of noise in quantum computing, and how it can help to overcome the challenges of noise in quantum systems.

Amazon Braket offers a fully managed, density matrix simulator, DM1, to simulate quantum circuits with noise. DM1 helps to investigate the effects of realistic noise on your quantum algorithms to inform error mitigation strategies to get more accurate results from today’s quantum computing devices.

DM1 is a fully managed, high-performance, density matrix simulator. We can use DM1 to simulate circuits with noise up to 17 qubits. DM1 is always available, executes your circuits on demand, and you can run multiple circuits in parallel.

As today’s quantum computers are naturally noisy. So every operation in a quantum circuit just introduces errors, causing the differences in the results of the computation.

In order to develop better algorithms that are more robust against the effects of errors, researchers need the ability to simulate noisy quantum circuits in a convenient and cost effective manner. And with the help of  Amazon Braket SDK, we can easily add custom noise models to new or existing circuits and run them with a single line of code on DM1.

Types of noise in quantum simulation

1. Dephasing: Dephasing is a type of noise that causes the quantum state of a qubit to lose its coherence, or phase relationship, with other qubits. This can cause errors in the measurement of the qubit, and can limit the accuracy of quantum algorithms.
2. Decoherence: Decoherence is a type of noise that arises from the interaction of a quantum system with its environment. It can cause the quantum state of a system to become mixed and disordered, which can limit the ability of the system to perform quantum operations.
3. Amplitude damping: Amplitude damping is a type of noise that causes the amplitude, or magnitude, of a qubit's quantum state to decrease over time. This can limit the ability of the qubit to store and transmit information, and can reduce the accuracy of quantum algorithms.
4. Bit flip: Bit flip is a type of noise that causes the value of a qubit to be flipped from 0 to 1, or vice versa. This can cause errors in the measurement of the qubit, and can limit the accuracy of quantum algorithms.

These are just some examples of the types of noise that can affect a quantum system, and there are many other sources of noise that can also impact the performance of quantum algorithms.

Noise simulation based on the density matrix formalism

In an ideal case, a quantum state prepared by a noise-free circuit can be described by a state vector |ψ⟩ , we call it a 'pure state'. However, the presence of noise in realistic quantum devices will introduce classical uncertainty to the quantum state. For example, a bit flip error with 50% probability acting on a qubit flips the |0⟩ state into either |0⟩ or |1⟩ with a 50-50 chance.Note that this is different from an Hadamard-gate acting on |0⟩: The latter results in a coherent superposition of |0⟩ and |1⟩, whereas the former is a classical, so-called mixture of |0⟩ and |1⟩. The most general way of describing a quantum state in the presence of noise is through the so-called density matrix.

The density matrix of a pure state is simply ρ=|ψ⟩⟨ψ| and, in the bit-flip example from above, the density matrix would be

p = 0.5 |0><0| + 0.5 |1><1|

The density matrix formalism is a very useful way to describe a noisy system with probabilistic outcomes. It gives an exact description of a quantum system going through a quantum channel with noise. Besides, the expectation value of an observable ⟨O⟩ can be easily calculated by Tr(Oρ), where "Tr" is the trace operator.

Let's try some noise simulations on using Amazon Braket Simulators.

Amazon Braket provides two density matrix simulators: a local simulator (braket_dm) that comes with the Braket SDK, and an On-Demand Density Matrix simulator (DM1).

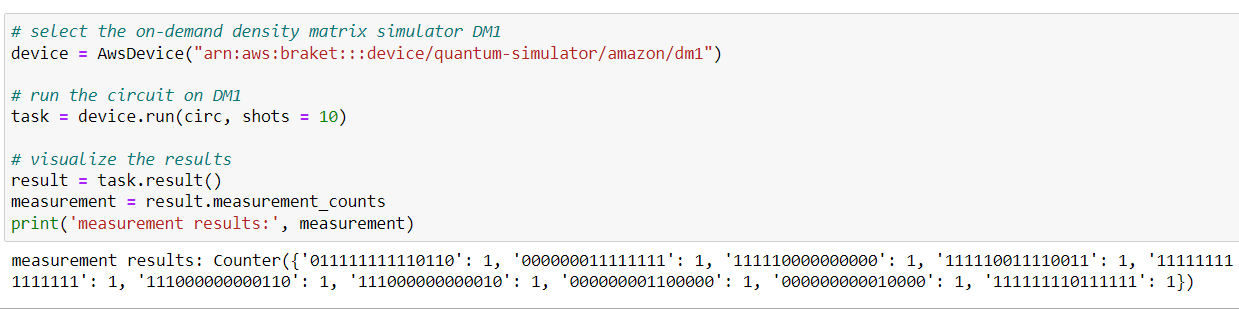
1- Let's see a very simple example of running a noisy circuit on Amazon Braket.

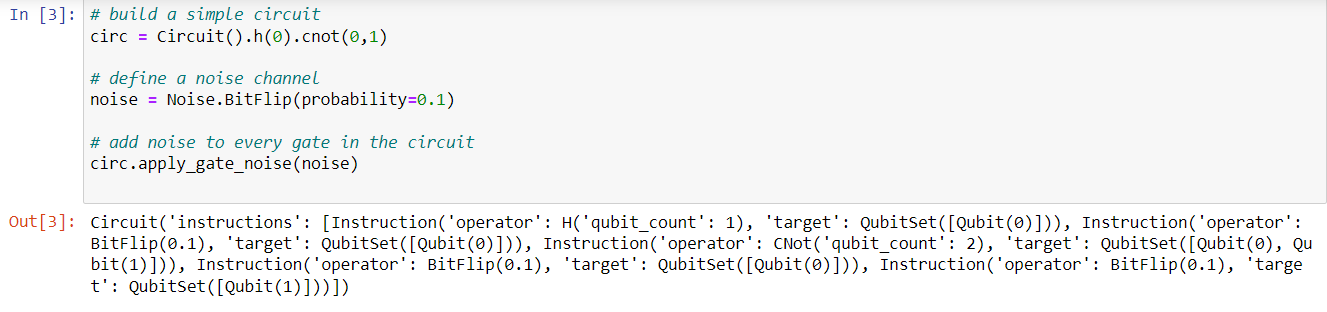
Note: apply_gate_noise function will add noise to each gate.

Output:

Note: Generally, in the noise-free case, here the circuit we had defined prepares a Bell-state, and we would expect to measure only '00' and '11' as the outcomes. But, the presence of noise, in our case a bit flip error, means that sometimes we find the state in '01' and '10' instead.

The local simulator i.e. (braket_dm) I have used above is suitable for fast prototyping on small circuits. If we want to run a noisy circuit with more than 10~12 qubits, it is good to use the on-demand simulator DM1.

2- So let's try for GHZ circuit and build a 15 Qubits GHZ-circuit

Note: Function to return simple GHZ circuit ansatz. Assumes all qubits in range(0, n_qubits-1)are entangled.

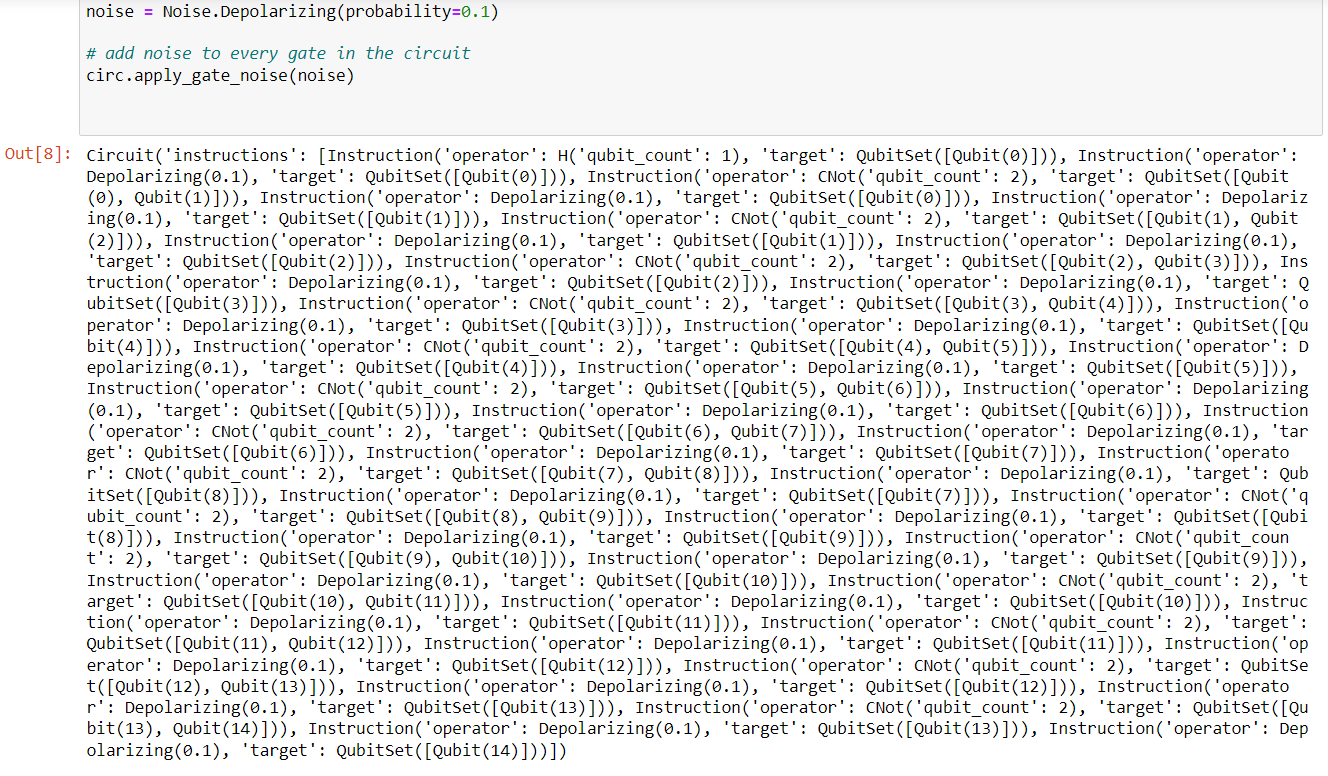
Note: the presence of noise, in this case is depolarising error.

Output:

The above code shows an example of preparing a 15-qubit GHZ state in the presence of noise.

Defining noise channels

In order to apply noise to a quantum circuit, we need to first define the noise channel, which is defined in Kraus representation(discusssed above). Amazon Braket offers many commonly-used noise channels in the Noise Class of the Amazon Braket SDK. In addition to this we can also define our own custom noise channel as a list of Kraus operators.

Pre-defined noise channels

There are some pre-defined single-qubit noise channels include namely  BitFlip , PhaseFlip , Depolarising , AmplitudeDamping , GeneralizedAmplitudeDamping,  PhaseDamping and PauliChannel

There are pre-defined two-qubit noise channels also which  includes TwoQubitDepolarizing and TwoQubitDephasing .

• Bit flip noise channel

This noise channel is equivalent to applying a bit flip error (modeled as applying an X gate) with probability p and doing nothing with probability (1−p). We can check the the target qubit count and the Kraus operators of the noise channel defined.

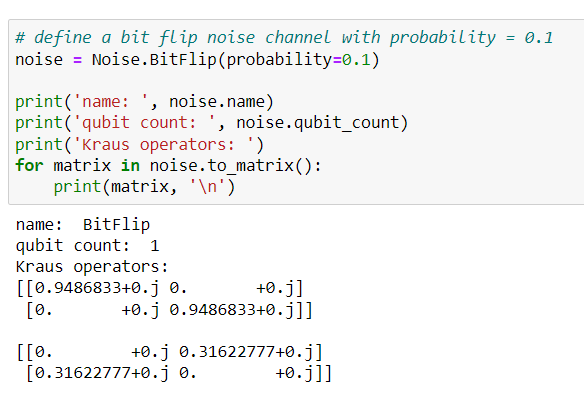
Let's check for one more noise error

2- GeneralizedAmplitudeDamping noise Channel

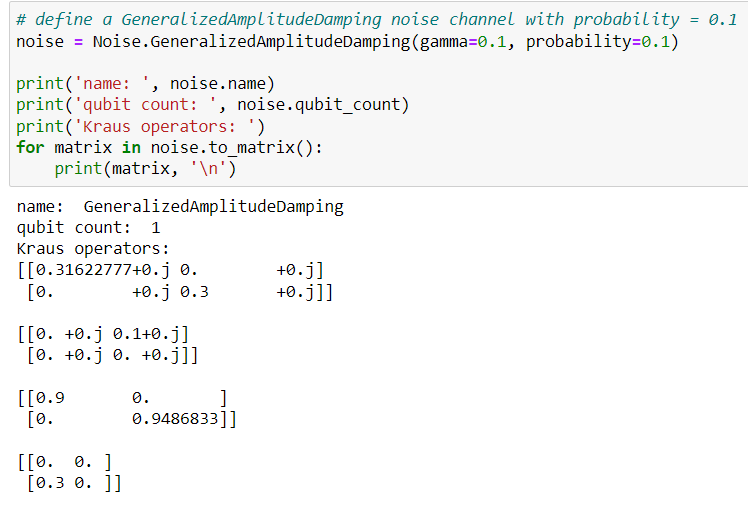
Other pre-defined noise channels can be used in a similar way.

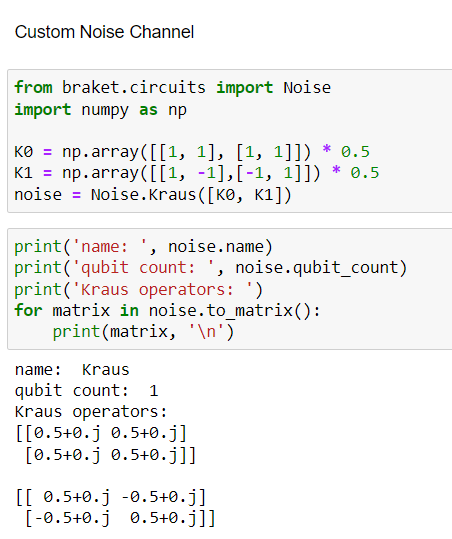
Custom noise channels

For example, one may want to simulate the behavior of a special quantum system that produces a type of noise that cannot be directly composed using the predefined noise channels. In this type of situations, it make more sense to define a custom noise channel.  In this case, it is possible to define noise channels with a list of Kraus operators. Each Kraus operator is represented by a matrix defined by the customer. The dimension of each matrix must agree with the number of qubits on which the custom noise channel acts.

For example, the matrix must be 2×2 for 1-qubit noise, and 4×4 for 2-qubit noise:

Adding noise to a circuit

There are two methods to build a 'noisy' circuit.

1- we can add noise to the circuit 'bottom-up', by using the noise operations in the same way as we  add a gate to the circuit.

2- we can use the methods apply_gate_noise() ,  apply_initialization_noise() and apply_readout_noise() to apply gate error, qubit initialization error and measurement error globally to existing circuits.

Error Correction Techniques:

To mitigate the effects of noises on the output of a quantum circuit, researchers and engineers are developing various techniques and error-correction methods to reduce the impact of noise on quantum systems. These techniques can help to improve the purity, predictability, and fidelity of the output of a quantum circuit in the presence of noise.

One of those techniques includes Quantum error correction codes. These codes encode the quantum state of a system using multiple qubits, such that errors in any single qubit can be detected and corrected.

Let's try one of the error correction code on Amazon Braket

As an example, let's evaluate the Bit flip error correction (repetition code) code, which is designed to resist bit flip noise by encoding a logical qubit into three physical qubits. This technique uses entanglement and syndrome measurements and is comparable in performance with the repetition code.

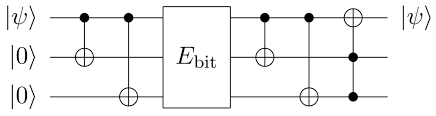
The following code snippet shows how we can test this code.

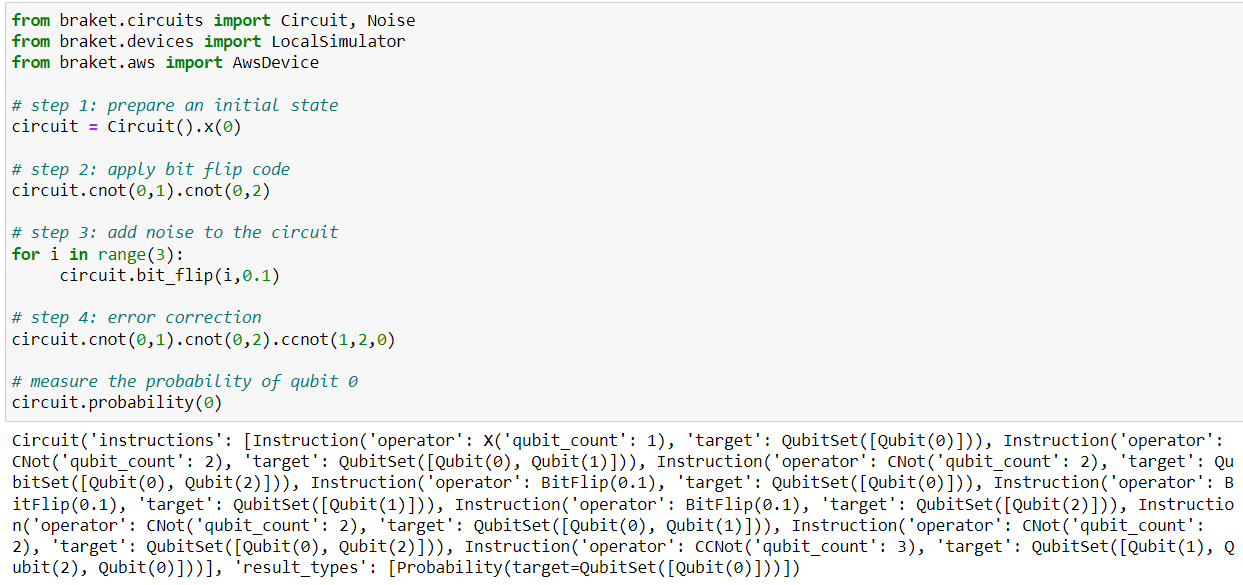
Note: 1- initialize the first qubit q0 into the state we wish to encode.

2-  We then encode this information by applying two CNOT gates to entangle qubit 0 with qubits 1 and 2. The encoding redundantly stores the initial state on qubit 0 across all three qubits.

If any of one of the three qubits undergoes a bit flip error, we can still recover the initial state by decoding the information. In practice, this is done by checking the parity between the different qubits, which tells us which qubit underwent a bit flip error, but without revealing or disturbing the encoded information.

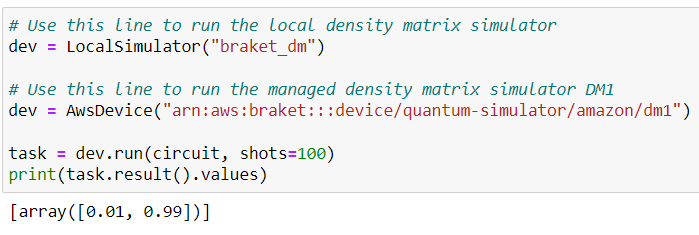
We can choose to run this circuit on a local simulator or on DM1.

After running the circuit on a density matrix simulator, the probability distribution of qubit 0 is [0.01 ,0.99] .

This distribution indicates that 99% of the circuit executions measure qubit 0 to be in the |1⟩ state and the error rate is 1%.

And if we skip step 2 and step 4 (i.e., skipping the error correction) the results are [0.2,0.8] which means 20% error rate which is more.

In other words,the error rate is 1% ,which is a reduction from the 20% noise rate of the bit flip error. This repetition code is able to correct up to one bit-flip error in the circuit, but not two or more bit-flips.

Conclusion

In this blog, we have learned how to create a circuit with predefined noise channels on Amazon Braket, such as the bit-flip and phase-flip channels, or custom noise channels for noise simulations. We learned that a density matrix simulator is required to perform noise simulations, and that one can use Amazon Braket local or on-demand density matrix simulators.At last we learned about error correction technique specifically Bit flip error correction or repetition code.